Home

Is Global Photosynthesis Broken?

The amount of Carbon dioxide in the Earth's atmosphere at any given time reflects a balance between production and consumption. The natural production of CO2 is estimated at 60 G tonne(C) per year.(note 1)That amount corresponds to a concentration change of 28 ppm/yr. The production of CO2 is balanced by the consumption--mostly photosynthesis (note 2). CO2 concentration has remained close to 280 ppm for thousands of years

The stability of the concentration with these inputs suggests a feedback process is at work. and we will study the effects of human caused changes in this feed back process--both fossil fuel burning and deforestation

The simplest feed back model is represented by the following differential equation:

In eq (1), Q(t) represents the rate at which Carbon Dioxide is introduced into the atmosphere. It is estimated that natural sources (excluding plant respiration and of course fossil fuel burning) are 60 G tonne Carbon equivalent annually. It is convenient to to express Carbon equivalent as parts per million of CO2 annually; that figure is about 28.25 ppm/yr. I take this figure to be constant.

The constant k represents inhibitory feedback: As plants continue to grow they consume carbon dioxide, lessening its concentration and that reduces the photosynthesis. On the other hand as oxygen respiring organism produce carbon dioxide that tends to increase photosynthesis activity which in turn produces more oxygen. Obviously the process is far more more complex then the simple model of eq (1), however for small deviations from equilibrium this linear model is the natural starting point and is certainly the easiest to calculate. Only experiment and observation will confirm the limits of validity. The purpose of this paper is to investigate how well eq (1).represents reality.

Presumably the global carbon cycle will reach a steady state (homeostasis) where dC/dt is zero. Taking Q=28.25 ppr/yr along with the estimated pre-industrial value of 280 ppm for the concentration C, leads to k=Q/280 =.1 yr-1. The solution for C(t) off equilibrium is easily seen to be:

Plotted For two different extreme hypothetical initial values of C(t)

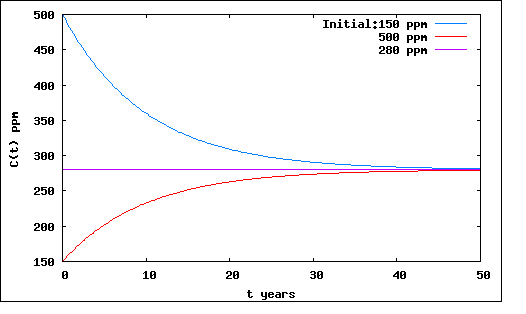
Fig. 1: Carbon Concentration,showing how feedback restores equilibrium

Note that it takes about twenty years to restore equilibrium for moderate changes. (Look at the range from 20 to 40 years)

We know that fossil fuel burning has increased the input of the CO2--that's the source term Q(t).

We are going to analyze the effects of the increased sources, and the effects of changing the feedback term K(t).

K(t) may be reduced from deforestation, for example.

First the sources from fossil fuel burning: Here is data from CDIAC. The data covers the range from 1750 to 2007:

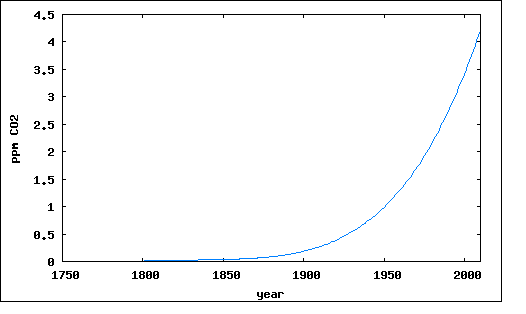
Fig. 2: Carbon Dioxide from Fossil Fuel

The curve in Figure 2 is best represented by the following polynomial:(note 3)

The function QFF represents an additional source of Carbon Dioxide, and should be added to the fixed natural source in eq (1):

Solution of eq (4) up to theyear 2010: (note 4)

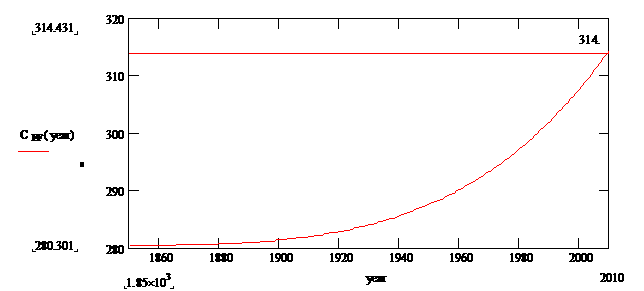
Fig. 3: CO2 levels including Fossil Fuel burning,k=.01 yr^-1,Q=28.25 ppm/yr

The CO2 concentration reaches a level of 314 ppmv by the year 2010, but the measured concentration is closer to 390 ppmv; so why the difference? A simple explanation is that the feedback constant k is decreasing mainly because of deforestation. Model a .2% annual decline in k since 1900 as follows:

2010 CO2 levels now reach 390 ppm.:

Fig. 4: CO2 levels with Fossil Fuel burning and declining k

Here is comparison with actual Mauna Loa CO2 levels since 1958:

Fig. 5 CO2 levels with declining k Calculated and Measured

Also, by calculating equilibrium values, we can say that even if deforestation and Fossil fuel burning stopped rising, starting today, the CO2 levels would continue to rise for about ten more years (1/k≈10 yr); the new equilibrium value would be 410 ppm.

However, if Fossil fuel burning stopped today, and deforestation continued at .2% per year, then CO2 levels would settle to about 460 ppm by the year 2050; A value of 480 ppm would be reached if fossil fuel CO2 continues to rise at the current 3% per year.

It does appear that photosynthesis can no longer maintain the historic 250-280 ppm level. In fact, even with the complete absence of fossil fuel burning the readings would be nearly 330 ppm by now:

So,in that sense the photosynthesis feedback process is indeed broken.

But what are the consequences of these elevated levels? Is there something special about the historic 280ppm concentration and doubling it will cause catastrophe?...or not?

It seems we have until 2050 to find out. Hopefully that's time enough

George Raetz

Home