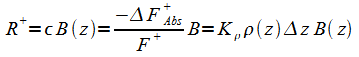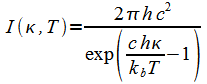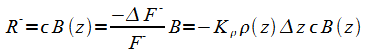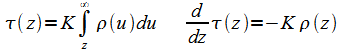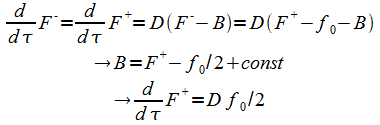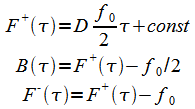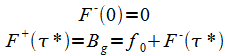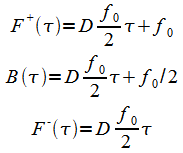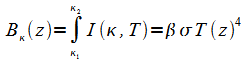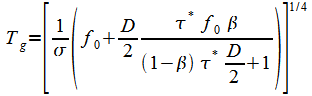Narrow Band Schwarzschild Radiation Balance Equations

Narrow Band Schwarzschild Radiation Balance Equations

A Simple Accurate Climate Model

How to Calculate Absorption from HITRAN data

Is Photosynthesis Broken?

CO2,water,pH

Ocean pH,Revelle effect(PDF)

Disable ActiveX

Why is Controlled Nuclear Fusion so Difficult?

Reaction Rate,Cross Section & Activation Energy

Quaternion Quantum Mecanics

Dirac Equation Solutions One dimensional spatial

Introduction

The radiation balance equations of K Schwarzschild describe how heat absorbing gasses in the atmosphere of a planet will warm the planet by trapping the heat re-radiated from the surface of the planet. The original theory proposed back in 1906 grossly overestimates the amount of warming. However a simple modification³ where the heat absorption is limited to a narrow band of radiation frequencies greatly improves the accuracy of the theory.
The first section of this derives the Schwarzschild equations in detail. Next they are modified for a narrow absorption bands; finally the modified equations are applied to the atmospheres of Mars and Earth. The calculations show a 25% increase of CO2 in the atmosphere of Earth will produce a surface temperature increase of about a tenth degree Celsius

Schwarzschild Radiation Balance Equations—Original wide band version

Figure 1 depicts radiation flowing thru a section of atmosphere of thickness Dz.

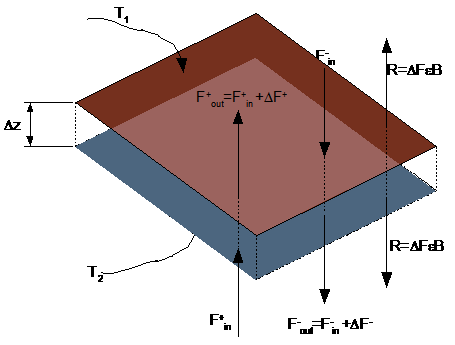
Fig. 1: Energy flow through a layer of atmosphere

The radiation flow is categorized into upward and downward flows F⁺ and F^-.Upward flowing radiation F⁺_in is entering the portion of absorbing-emitting material. A portion DF=F_out-F_inis absorbed by the material; The amount of radiation energy absorbed is proportional to the distance,Dz (positive going upwards) and is also proportional to the the radiation intensity itself:

	(1)

The absorbed radiation is re-emitted as R⁺ in accordance with Kirchhoff's law; The total upward flowing radiation on the outbound side of the block is comprised of the incident radiation less that absorbed plus the radiation R that is emitted from within the block. The intensity of the emitted radiation is:

	(2)

Where DF from (1) is substituted into (2), and the fraction of energy absorbed is equated to the emissivity according to Kirchhoff law. Use a minus sign because DF is negative for absorption.

Generally, B(z) is related to Planck's function. For wide spectral bandwidth situations in gray-body type atmospheres, B(z) is taken as Planck's function integrated over all frequencies—the Stefan-Boltzmann function:

	(3)

If the frequency k is measured in wave number units, then Planck's function I(k,T) is:

	(4)

R⁺ in (2) adds to F⁺ in (1):

	(5)

For the downward flowing energy we have:

	(6)

Sign changes in (6) because Dz from F^-_in to F^-_out is negative. The downward version of (2) becomes:

	(7)

Substitute (7) into (6) to get the downward version of (5):

	(8)

The differences become differentials in the usual way in (5) and (8)to get:

	(9)

	(10)

Up to now, only the energy flow in two directions—up and down have been considered. Obviously, energy can flow in any direction. For the situation of a planet atmosphere, where the radiation is locally isotropic, it's possible to integrate equations (9) and (10) over the possible directions and that leads to the simple modification:

	(11)

	(12)

The constant D is generally taken to be 3/2 though other values are used. This is a standard part of the theory and is discussed in the book by Goody and Yung for example. It turns out in the that the final value of temperature is not very sensitive to the value of D in the narrow band modification.

Change of Variable z to Optical Depth t

As long as K_r is constant so that the absorption is only a function of the distance z, (11) (12) can be rewritten in a solvable way through the introduction of the optical distance variable t defined as:

	(13)

Variable t is dimensionless and physically represents the logarithm of the relative radiation attenuation over the distance z. Since r decreases with increasing z, t also increases with increasing height. Writing (11) (12)in terms of t:

	(14)

	(15)

The energy fluxes F^± are not independent. Their sum equals the externally applied radiation source f₀(the Sun in other words):

	(16)

So with the help of (16) we can eliminate F- to get:

	(17)

And the general solution of(14) and(15) is

	(18)

The constants are determined from the boundary conditions:

	(19)

With t* being the mapping at zero height:

	(20)

From definition (20) together with boundary condition (19) into (18):

	(21)

Temperature is determined from (3).

Schwarzschild Radiation Balance Equations--Narrow Band Absorption

These equations with some modifications (Weaver and Ramanathan ³) can be applied to portions of the spectrum provided that Kirchhoff's law holds on a frequency by frequency basis. We consider the case where absorption takes place over a limited range of frequencies. The emitted power (3) becomes:

	(22)

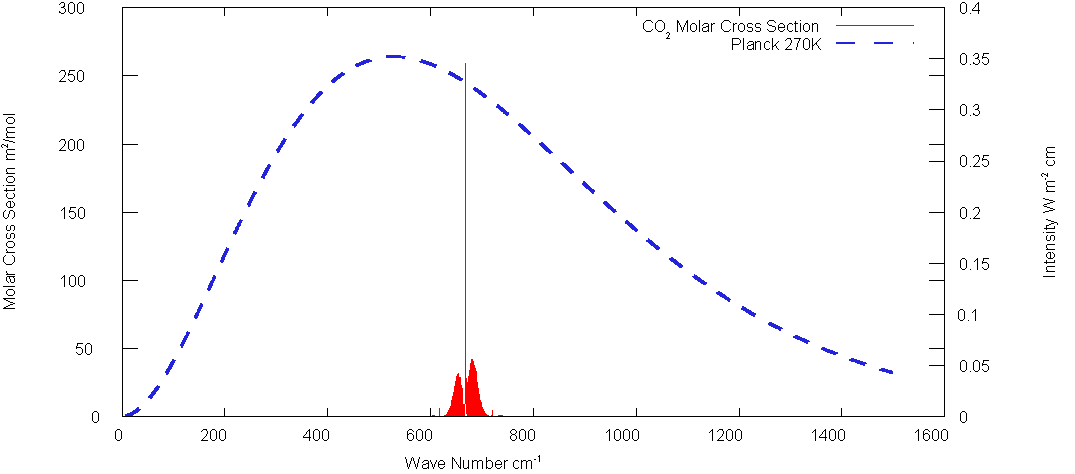
Fig. 2: CO₂ Spectrum

eq. (22) defines b which is a function of temperature owing to the changing shape of Planck's distribution with temperature. As a simplifying assumption, take b constant.

The energy balance equation (16) is modified—the difference between upward and downward energy flux is no longer the total energy input from the Sun, but a fraction thereof to be determined from the boundary conditions.

	(23)

Generally, f''₀ is temperature dependent, but again simplify to a constant.

Equations (18) are likewise modified:

	(24)

The boundary conditions are:

	(25)

Note that f₀ is not primed in (25) because we assume the ground absorbs all the radiation( 95% for earth though it's easy to allow a an emissivity <1.); only the fraction b is available for atmosphere absorption. From (24) and (25):

	(26)

From Eq.(22), the temperature as a function of optical depth is:

	(27)

To obtain the ground temperature use t* in (27). to get:

	(28)

Applications

Carbon Dioxide parameters:

There are actually two relevant absorption bands for CO2 which are evident the following plot of Fig. 2 on a log scale(The band at about 2500 cm1- is totally outside the 270K spectrum).

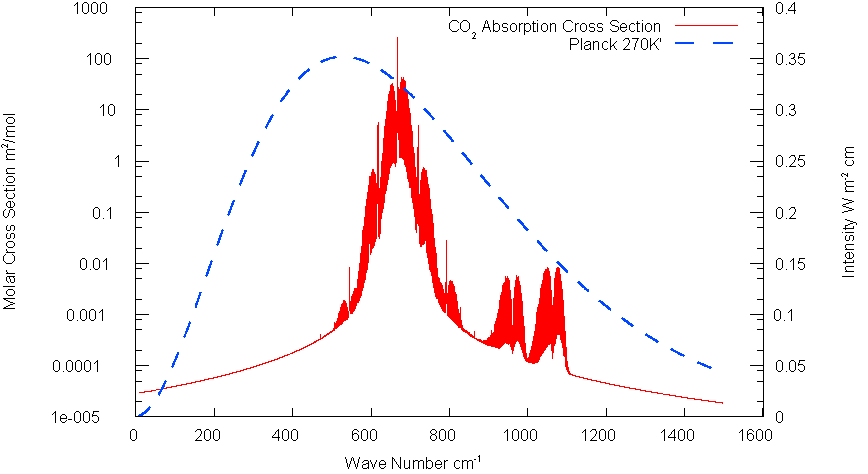
Fig. 3: CO2 Spectrum Log Scale

The specific cross section K which defines t eq(13) is applied only to the absorbed band of frequencies. Value calculated from HITRAN data is 5.25 m²/mol for a band 200 cm ^-1 wide centered about 667cm^-1.(Half width 100 cm^-1)The parameter b of eq. (22) is about .108. for this bandwidth. The band centered at about 1050 cm^-1 has specific cross sec tion of only about 7x10^-4cm²/mole.

Calculate optical depth

For simplicity, take temperature as constant T_avg in the hydrostatic relation:

	(29)

R_m is molar gas constant; g is gravity acceleration,M_CO2 is molecular weight of Carbon Dioxide.

The optical thickness (20) at ground level works out to be:

	(30)

Where K_k is the specific molar cross section applied to the band of absorbed frequencies;p0 is the surface pressure.

Example: Mars

Mars is a good place to test the theory as its atmosphere is 95% carbon dioxide. The surface pressure is only about 600 Pa—less than .6% that of Earth,but it would stack to a height of over 80 meters if squeezed to STP conditions. By contrast, Earth's CO2 component at 380 ppmv would occupy a height less than 2 meters under the same conditions. So if one compares the respective CO₂components, the Mars atmosphere is actually very thick relative to that of Earth. Calculation parameters are shown in table 1. Two values of D are used. They bracket the various accepted values and have little effect on the surface temperature. The bands at 667cm^-1 and 1050 cm^-1 warm the planet about 6K and 4K. Add the two to the black body temperature to get a surface temperature of about 222K.

Table 1: Calculation Results

Earth

At 380 ppmv(300K), the calculations shows that carbon dioxide warms the atmosphere about 7.37. This band s saturated; if the concentration were raised to 500ppmv the warming would only increased to 7.38K. The band at 1050cm-1 contributes about .3K warming and that would increase to about .4K at 500ppmv.

Table 1 also shows the calculated effect of water vapor. There are two areas of absorption; the main band is centered at roughly 250 cm-1 and contributes nearly 24 K warming. The other band though much wider, is located on the tail of the Planck spectrum and contributes only about 6 K warming.

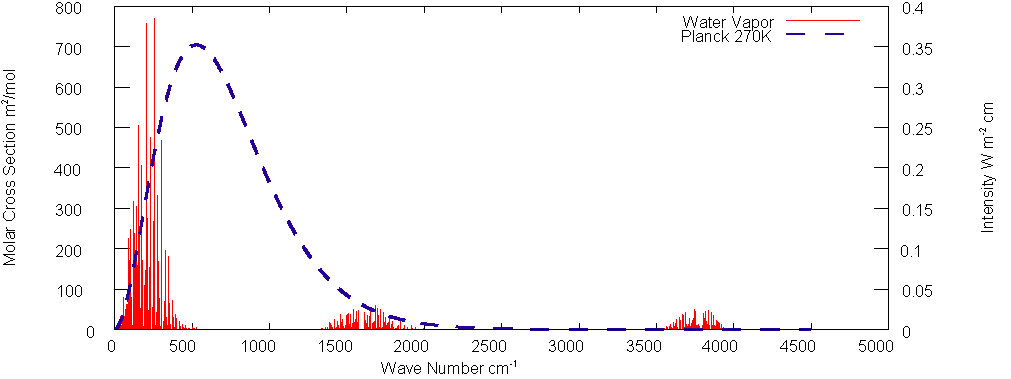
Fig. 4: Water Vapor Absorption

Atmospheric Temperatures

Write the optical thickness parameter t as a function of height using the simplified hydrostatic relation 29:

	(31)

Using only the water vapor data in eq. 27 and 31:

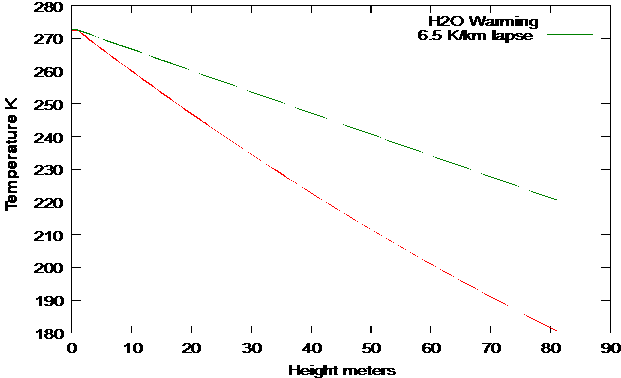
Fig. 5: Predicted and Actual Lapse rate

We see that the actual temperature lapse rate is significantly less than the theory. But that is to be expected. The adiabatic cooling rate induces instability in the atmosphere and that's what makes a changing climate. The details of the process are beyond the scope of this theory.

Conclusions

This simple modification of the classic Schwarzschild equations to allow for limited absorption bandwidth of the heat absorbing gasses in an atmosphere produces excellent agreement with observations on both Earth and Mars. The calculations also show that a 25% increase of CO2 in the atmosphere will produce a temperature increase of about .1 °C.

References

1. Goody ,R, M. and Y.L. Yung, Atmospheric Radiation:Theoretical Basis,2^nd ed. Oxford University Press, New York, 1989.

2. Pierrehumbert, R.T. Principles of Planetary Climate

http://geosci.uchicago.edu/~rtp1/

3. Weaver, C.P. Weaver and V. Ramanathan, Deductions from a simple climate model: Factors governing surface temperature and atmosphereic thermal structure, J. of Geophysical Research v.100 no. D6 pages 11585-11591