HOME

Reaction Rate and Activation Energy

Two species of molecules are at concentration n1 and n2. (typical unit: molecules/m3). They are confined to a volume V and at temperature T. They undergo a binary reaction, with cross section σ(v), where v is the relative velocity of the molecules. The reaction rate is:

In (1) f₂ is the joint probability density function for two values of the velocity. The inner integral (over v₂ in this case) counts the number of particles moving at velocity v₂ while the second counts and weighs those at a given v₁-v₂

If there is only one species of reactant (eg the nuclear fusion reaction of pure Deuterium), the integrals will double count the number of reactions. In that case replace the product n₁ n₂ with n²/2, n being the number density of the single reactant. In the case of a dilute gas at equilibrium, this joint probability density function is the product of the values of Maxwell-Boltzman distribution at the the two velocity values.

We need to integrate over the relative velocity, so make the following change of variables:

Note the Jacobian of the transformation is unity so:

First expression in brackets is unity, rate per unit volume is:

For the case where the cross section depends only on the magnitude of the velocity not the direction:

When the particles are identical, n1=n2=n, there is a double counting so in this case:

If the cross section is a function of the relative kinetic energy E, then make the following substitutions

For nuclear fusion reactions, the dependence of cross section on energy (or speed) may be a narrow peak. A minimum energy is needed to break the activation barrier, but if the relative velocity of the molecules is too great they will go by each other, like a fast moving comet may miss a planet while a slower one may be captured. If the dependence of cross section on relative kinetic energy is a narrow peak of width DE_A , centered about E_A then:

Equation 10 is a generalized Arrhenius rule:

In the case of chemical reactions,the usual references restrict n to between ±1. So the result in 10 disagrees with the conventional formulations. so try a different simplifying assumption for the dependence of cross section on relative speed: The cross section is zero up to a minimum relative energy then rises to a constant value and stays there for all higher relative speeds. something like this:

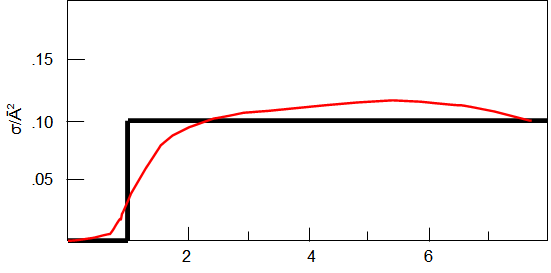
Fig 1: Step function Cross Section in square angstroms, energy in ev.

The integral in (6)evaluates to:

A sum of two terms, each of the Arrhenius form(11).

A plot of (12):

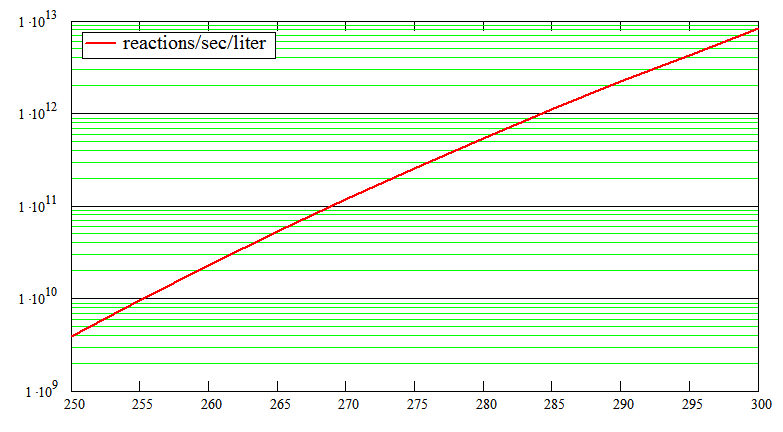
Reactions per liter per second against Temperature(K)

Experimental verification would be welcome, but in practice reaction rates are difficult to measure accurately. Mixing time and dilution from the products allow only approximate values.

HOME