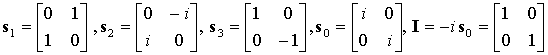(1)Start with the Pauli spin matrices as a Quaternion basis:
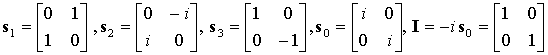(1)
Instead of the basis s0,s1,s2,s3 use I,s1,s2,s3 . Define:
(2
Also define the surface bivector units:
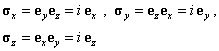(3)
It is possible to
avoid the imaginary unit i in all equations including the Dirac
equation with the help of these bivector units . The imaginary unit
is mathematically convenient however, and most people are used to
seeing it. For that reason, what I’ve done is to group i
with the appropriate line vector. When you see i ez
for example, mentally replace it with
Also
see the section on Clifford Algebra.
Let
be
quaternions (the coefficients may be complex) then define the vector
conjugate
(4)
and Hermitian conjugate
(5)
In matrix form we can write:
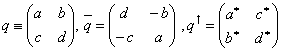(6)
There is a four-vector dot product and a space-time scalar product:
Given q=q0I+qxex+qyey+qzez to find q0,qx,qy,qz use:
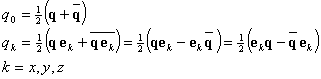(8)
Magnitude of a quaternion, scalar part ,vector part of quaternion ,‘unitizing’ operator U ,and angle of a quaternion.
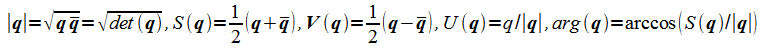(9)
Note that the magnitude of a quaternion is not necessarily real or positive. The unitizing operator U converts all quaternion to a quaternion with magnitude equal to positive one.
(10)
If the quaternion is written as a 2x2 matrix then the following equivalent form is computationally useful {error: use V(q)}
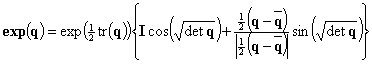(11)
Also useful are the logarithm and the square root:
(13)
A location r in space-time is represented by a quaternion with real coefficients:
(14)
r is Hermitian r†=r. (because the coefficients x,y,z,t are real) r is said to be time-like, light-like or space-like depending on whether |r|2=det(r) is >0 ,=0 or <0.
Consider a
Quaternion L of unit norm:
,
Then a Lorentz transform of an Hermitian quaternion r is
Eq (15) represents only homogenous Lorentz transforms that are proper(preserves spatial parity or ‘handness’), and orthochronous(preserves time direction)). It’s obvious that multiplying L by a complex number of the form
won’t
change the Lorentz transform at all. It is most convenient to
choose the parameters so that |L|=1 and the scalar part of L
is pure real. Or det(L)=+1 and Im(Trace(L))=0.
If L happens
to be Hermitian:
then
L effects a pure velocity transform If
then
we have a pure 3D rotation (see below) .
The Lorentz transform preserves the space-time norm of any quaternion:
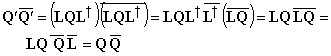(16)
To rotate thru the
angle
about
a unit axis
(note that
,
alternatively one could use the axis
that
would remove the factor of i in the rotation formula and
introduce a factor of i in the Lorentz formula but that would spoil
the geometric interpretation. Note that
i a is the unit bivector defining the plane of rotation)
use the quaternion:
Then the rotation is
(Right hand rule:
point thumb along a curl fingers in direction of positive)
To effect a Lorentz
transform of speed v along the unit axis:
(That is: transform to a frame where an object that was at rest, in the initial reference frame now appears to move at velocity v in the new reference frame)
First, let
,
then use the quaternion
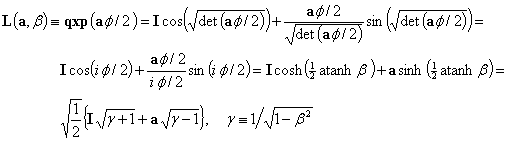
The Lorentz
transform of q is
For the space-time
event
,
the coordinates will transform to
(For a velocity in the opposite direction (-v/c) replace a with –a in the expression for L)
Find the Lorentz transform that ‘rotates’ space-time event A into B. That is for unit Hermitian quaternions A and B find L such that:
Then
(Note that A and B must be Hermitian and time-like)
As mentioned det(L)= +1 and the scalar part of L is pure real. With these restrictions, the most general form of L is
where aL
and aR are real (Hermitian) unit
three-vector quaternions of the form
and
are
real numbers. These six independent parameters together with
det(L)=+1 and Im (Tr(L))=0 determine the
eight components of L, Use the quaternion logarithm function
(12) to find these parameters. The usual rule for the product of
exponentials generally does not work for quaternion exponentiation,
however through Singular Value Decomposition L can be factored
into:
That is any Lorentz transform can be resolved into a rotation followed by a boost along the z axis followed by another rotation. Formulas for the parameters in (18) are exceedingly complicated and won’t be written here. They can be obtained from any good symbolic algebra program—just apply SVD to a general complex 2x2 matrix.
So to get a product of Lorentz quaternions L1 L2..Ln into the form (17), use the logarithm function. To get the canonical form
(18) use singular value decomposition.
Let S(t,x,y,z) be a
scalar valued function of the coordinates that is, some field takes
on the value S(t,x,y,z) at the space time point
.
The gradient operator connects the values at neighboring points. Let
be
the usual small displacement from r then in terms of the
ordinary gradient
we
write:
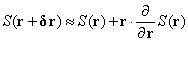(20)
To get the same expression in terms of the quaternion gradients of (19) we use the scalar dot product (7a)
(The second line is a notation convention)
Next, consider an Hermitian quaternion-valued field Q(r):
(22)
Let a be the three vector with real components (ax,ay,az),The quaternion gradient combines the gradient, divergence, curl :
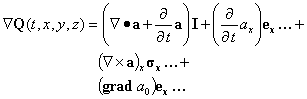(23)
For a anti-hermitian quaternion
(24)
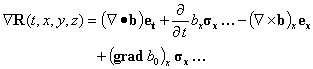(25)
The quaternion gradient can be defined as a volume integral:
(26)
Here, dx,dy,dz,dt are quaternions understood to be dx ex with dx a scalar and so forth.
Reference: J Scott: Complex four-vectors and the Dirac equation
A good paper. Some of his terminology is a little different from mine. For example his term quaternion corresponds to Hermitian quaternion.
In the original form as described in the Principles of Quantum Mechanics, Dirac defined the following 4x4 matrices, Portray them here in block-partitioned format.
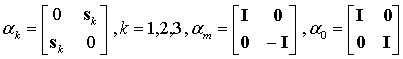(27)
The four-vector
wave function
evolves
according to:
We can also write this as:
Let
Define:
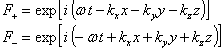(31)
Then
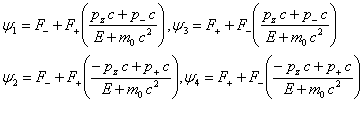(32)
Define the following quaternion:
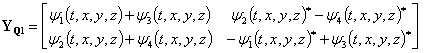(33)
Then either (28) or (29) is equivalent to:
To solve (34), apply the Lorentz transform to the particle at rest solution:
(E,p,w are defined in(30))
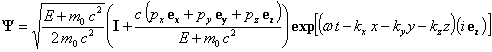
(This normalization
makes
).
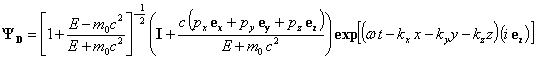
(This normalization makes the probability density r=1. see below).
There is also a time reversed negative energy solution to (34).
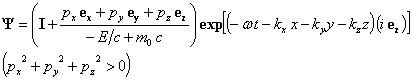(36)
Also note
that
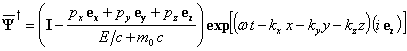(37)
Through simple algebra, we get the following variations on (34).
Furthermore, let
Eq (34), (38b) and definitions (39) can be combined into:
The advantage of the last form is that it avoids the conjugate of the wave function. It doubles the number of equations and might be explored as a generalization of the Dirac equation. Eq (39) and 35 (35) are special solutions. These equations were first discovered by Lanczos and Proca in the 1930’s, later rediscovered by others.
Another advantage of (40) is that we can most easily relate it to the QRW process.
Let
(41)
be the probability
current. J is an Hermitian quaternion so the components r,
j are real. (note that
is
Hermitian but
).
We should be able to prove from the Dirac equation (34) that:
(42)
but I can't find a
direct proof. The best I could do was to numerically differentiate
randomly chosen quaternions and check (42) that way.
Or, argue
that (28) and (34) are equivalent, so they should both lead to (43)
below. And thanks to Dirac, we know that (28) leads to (43).
From the four-vector
dot product formula (7a) and (42)it follows
that:
(43)
To summarize: the
probability density is the scalar part of the quaternion
(44)
.
The probability
current is the vector part of J:
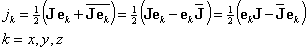(45)
(Second equality: conjugate(Q)=-Q if Q has no scalar part)
(7)
(12)
(15)
(17)
(18)
(19)
(21)
(28)
(29)
(30)
(34)
(35)
(38)
(39)
(40)