Back(to quaternion mechanics Table of Contents

Clifford Algebra

You can find a good tutorial on Clifford algebra in

http://www.mrao.cam.ac.uk/~clifford/introduction/intro/intro.html

(Stephen Gull et al., Imaginary Numbers are not Real-- the Geometric Algebra of Spacetime)

This brief summary is limited to the application of 3D clifford algebra to relativity.

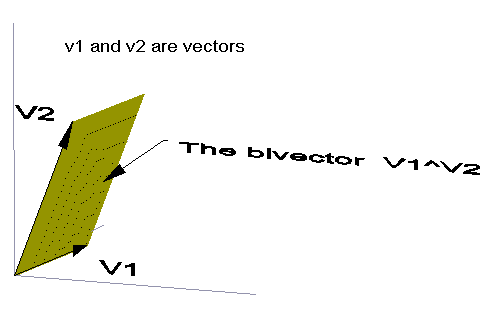
Everyone knows that from two vectors V₁ and V ₂, one can form the dot product or scalar product V₁ ^. V₂: Multiply the length of one vector by the normal projection of the other. One can define another product in terms of the parallelogram defined by the vectors--pictorially:

Call this the wedge product and denote it as V₁^V₂. Note that the parallelogram itself is the wedge product:not the area (that equals the magnitude V₁^V₂). Nor do we associate a vector with the area as we do with the vector cross product. If we flip the parallelogram around, we would be looking at V₂^V₁; that suggests that V₁^V₂=-V₂^V₁. The most general product of V₁ and V₂ is the combination of these two--call this the geometric product. The symmetric part of the geometric product is the dot product; the antisymmetric part is the wedge product.

V₁V₂+V₂V₁=2V₁^.V₂

V₁V₂-V₂V₁=2V₁^V₂

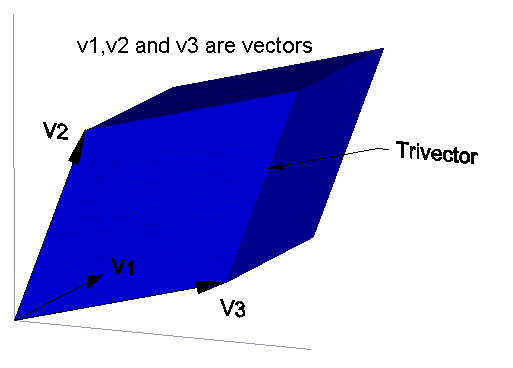
The geometric product of three vectors V₁,V₂,V₃ is a mixture of a vector and a paralellepiped trivector:

V₁ V₂ V₃=(V₁ ^. V₂)V₃- (V₃ ^. V₁)V₂+ (V₂ ^. V₃)V₁ +trivector

The trivector can be isolated as the antisymmetric part of this product:

trivector=(V₁ V₂ V₃-V₁ V₃ V₂-V₂ V₁ V₃+V₂ V₃ V₁+V₃ V₁ V₂-V₃ V₂ V₁)/6

If we define the wedge product to be the antisymmetric part of the geometric product then we can say that

trivector= V₁ ^ V₂ ^ V₃

It is easier to work with an orthormal basis.

In three-space, define three orthonormal unit vectors e_x,e_y,e_z. From these unit vectors form three unit bivectors.

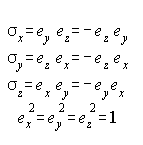
Also from the three unit vectors we define the unit trivector (Note that we don't have to antisymmetrize the geometric product of the three basis vectors to get the trivector because the basis vectors are all perpendicular to each other):

From the symmetry properties of the geometric product we calculate the square of the unit trivector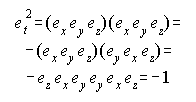

So e_t behaves like the imaginary number i.

We can also calculate the product e_t with the unit vectors. For example

Continuing this way we find that the three unit vectors of ordinary three dimensional space e_x,e_y,e_z together with the unit trivector e_t (which is defined from the three dimensinal unit vectors)have exactly the same algebra as the unit Pauli quaternions s₁,s₂,s₃,s₄ of complex four dimensional space! (This may not be as surprising as it first appears when considering that the time intervals may be defined as events connecting spatial intervals with light signals). This means that the geometry of space-time, conventionally thought of as four dimensional can be described with three dimensional geometry. We start with the Lorentz transform:

Lorentz transformation in three dimensions

Let an event occur at a spatial location defined by coordinates x,y,z and at time t with respect to a cartesian reference frame formed with unit vectors e_x,e_y,e_z taken to be at rest. Associate with this event the following vector-scalar object:

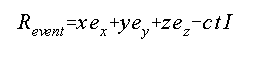
(I is the unit scalar defined in terms of the dot product of a unit vector: e_x e_x=e_ye_y=e_z e_z=I)

Now, transform to a reference frame with velocity v; Define the following vector-scalar Lorentz transform object:

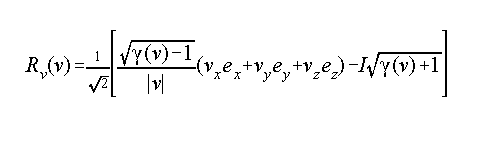
where

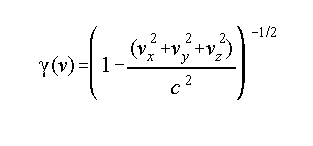
Then the vector-scalar event object in the moving reference frame is

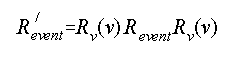
Rotations in three dimensions

Let a and b be vectors of unit length. To effect a rotation from a to b in the plane defined by a and b, first define:

Then, to rotate any vector x to x':

For instance:

R(a,b) is called a rotor and is a scalar-bivector object. In three dimensions, a rotation can also be defined by a rotation axis n,and a rotation angle about this axis; the corressponding rotor is:

Back(to quaternion mechanics Table of Contents