 (1)
(1)We start with the following one-dimensional form of the free particle Dirac Equation
 (1)
(1)
The
wave function ![]() is a complex two component vector:
is a complex two component vector:
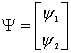 (2)
(2)
The probability density is:
![]() (3)
(3)
(That is to say the
probability of finding the particle in a space time region is ![]() )
)
The ![]() can be represented as complex matrices with the conditions:
can be represented as complex matrices with the conditions:
![]() (4)
(4)
Amongst numerous possibilities we will use:
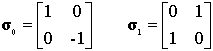 (5)
(5)
The equation can be written out as:
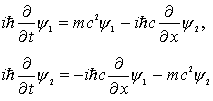 (6)
(6)
It is easy to show from the differential equation that:
![]() (7)
(7)
Where: the current J(t,x) is
We categorize two types of plane wave solutions, according to positive or negative energy: Let
![]() (9)
(9)
(Throughout this article the square root function is taken to be the branch with positive real part)
![]() (10)
(10)
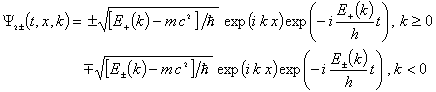 (11)
(11)
Just as in non-relativistic theory the energy and momentum operators are:
![]() (12)
(12)
The eigenvalue of these operators
![]() (13)
(13)
are related by the ‘classical’ relativistic expression
![]() (14)
(14)
In Dirac theory the negative branch of the square root leads to negative energy solutions
It is easy to verify (but follow the rule on the square root branch strictly and carefully) that
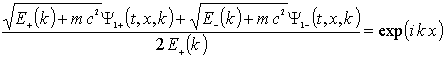 (15)
(15)
![]() (16)
(16)
We can now construct
various wave packets with the ![]() component initially zero and with arbitrary initial
component initially zero and with arbitrary initial ![]() component.
For example this wave packet starts with the
component.
For example this wave packet starts with the ![]() component
a real gaussian and
component
a real gaussian and ![]() .
.
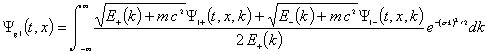 (17)
(17)
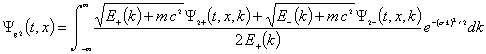 (18)
(18)
(Move
the mouse cursor over the graphs to start the animation. you must
enable GIF animation and JavaScript in your browser)
First a wide wave
packet: the width parameter ![]()
On the animation you will notice an oscillation imposed on the overall spreading of the packet. This oscillation is sometimes referred to as zitterbewegund (jitter-motion) the oscillation frequency is mc2/h
If the initial width of the packet is smaller than the wavelength of this oscillation than the wave packet evolution is surprisingly different:
The negative energy solutions are unphysical in nature; it would be nice to form gaussian wave packets using only the positive energy solutions. This we can do, but we can’t set the both components to arbitrary initial conditions: there aren’t enough degrees of freedom.
We can however, start out with zero current and real gaussian probability distribution as follows. First,note that
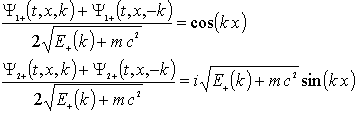 .
(19)
.
(19)
The first expression is real the second expression is imaginary so the current is zero(see eq8). We form a wave packet that is gaussian like initially with zero current:
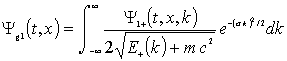 (20)
(20)
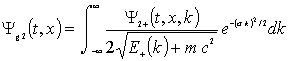 (21)
(21)
Again, animations, first
with a relatively wide wave packet with ![]()
The main qualitative difference here is that the zitterbewegund is not visible in the probability distribution.
Again the narrow packets split up and travel at about the speed of light: The physical reason for this behavior lies in the uncertainty principle. The extreme localization to a distance smaller than the Compton wavelength imparts large momentum. to the particle
If you have MathCad 8 or higher, you may wish to examine the file that generated these graphs(about 60Kbyte): Dirac1Dwp.mcd